Skip to main content

横向联邦Paillier方案

1. 简介​

  1. 假设有两个client，称为client1和client2

  2. 各client在密文状态下训练，将添加随机数的密文模型参数发送至server

  3. server聚合模型参数，并拥有私钥，可以解密聚合后的密文模型

2. 算法步骤​

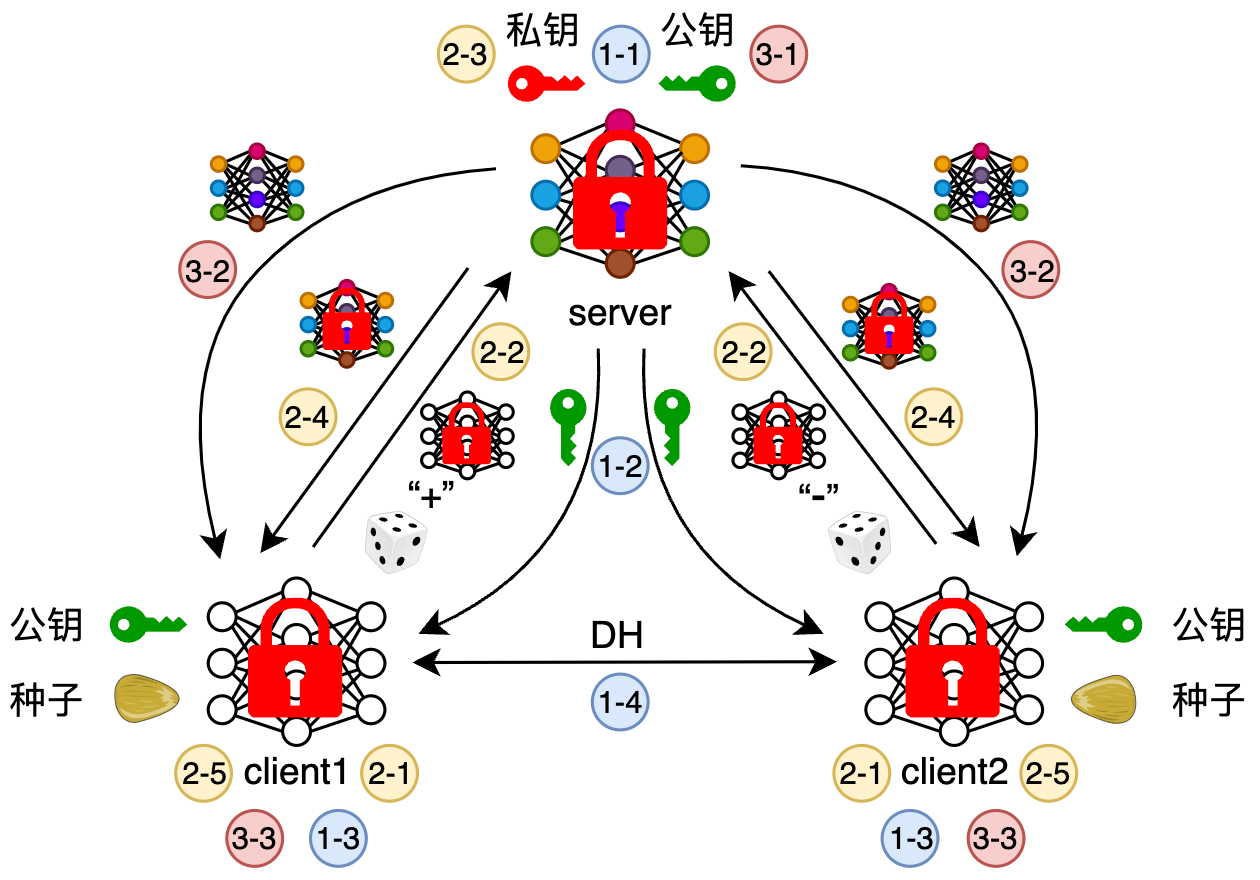
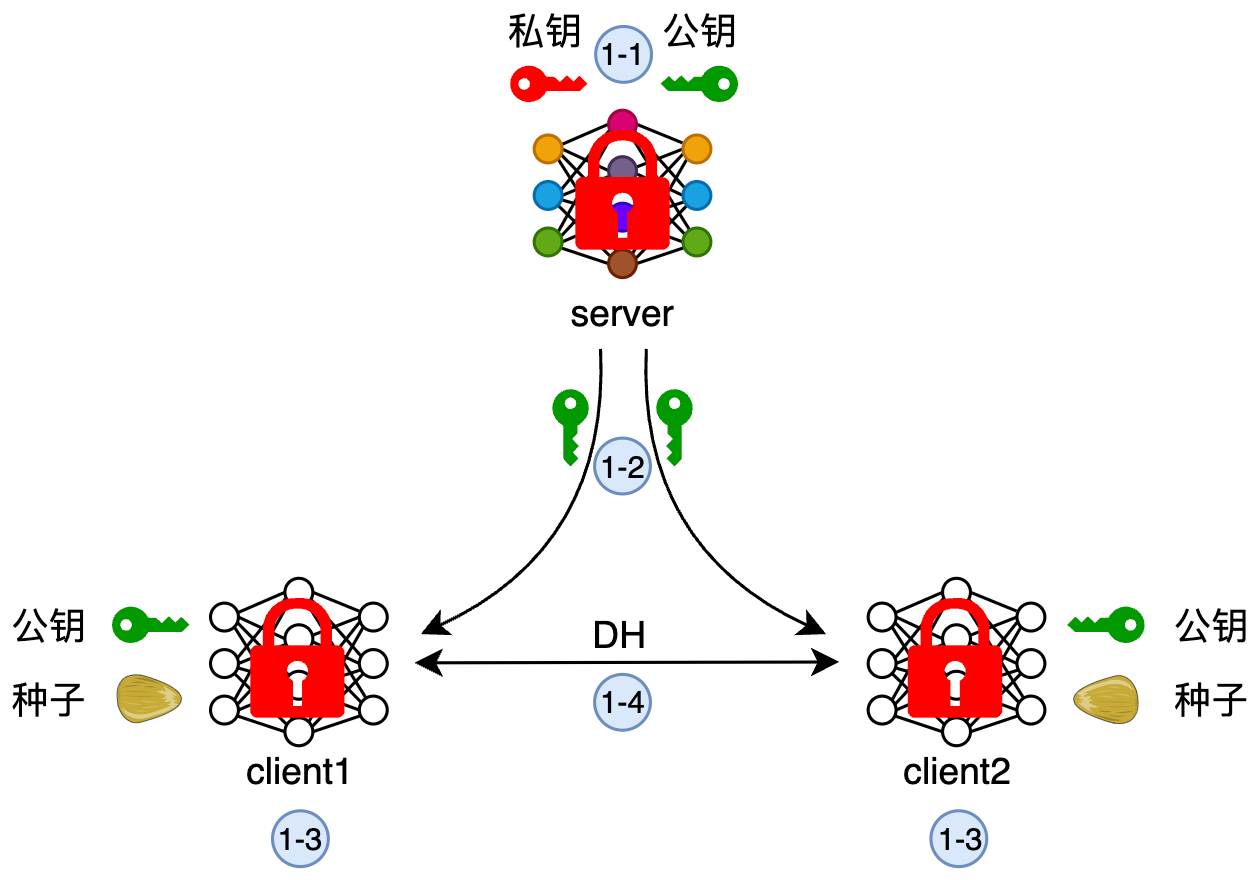
阶段1：参数交换​

  1. server基于Paillier库生成公私钥对

  2. server将公钥发送给各client

  3. 各client初始化模型参数，并使用公钥将模型参数加密

  4. client1和client2基于DH密钥交换协议生成随机数种子

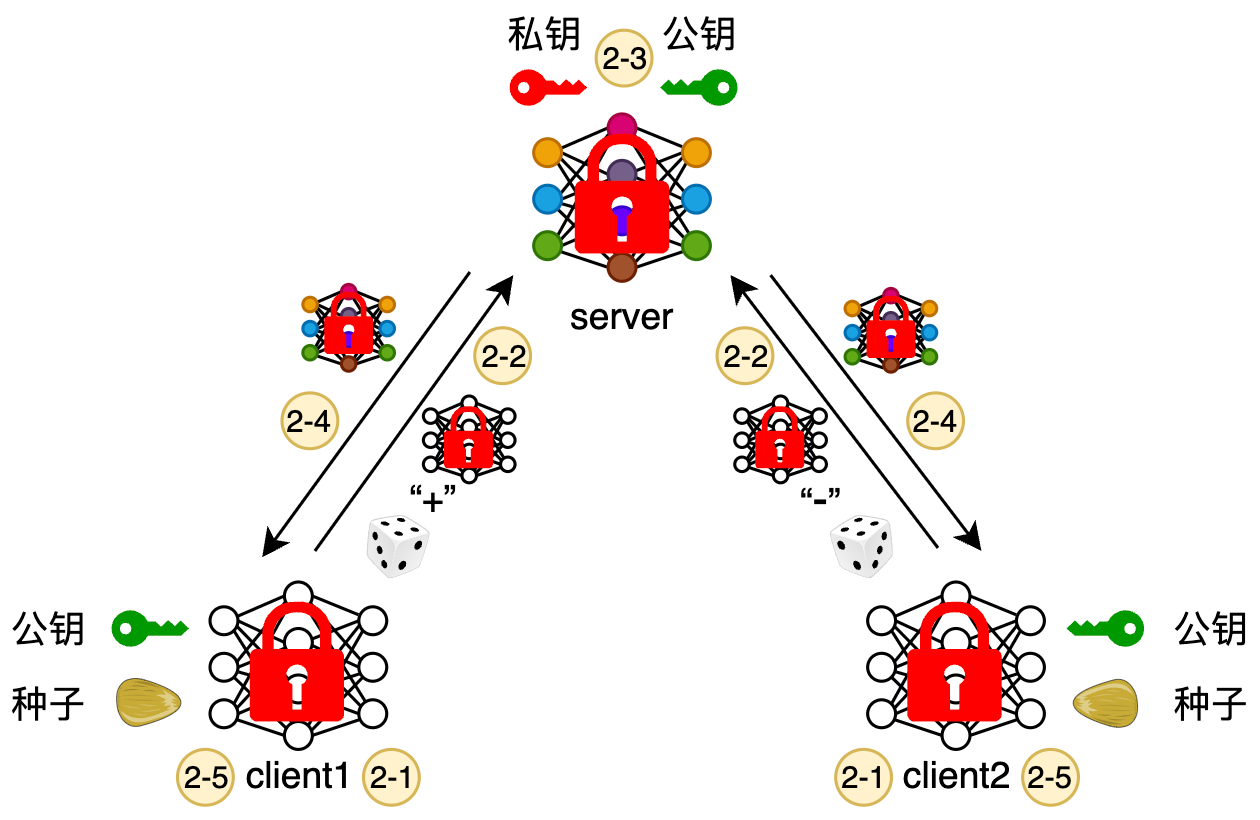
阶段2：模型训练​

  1. 各client使用本地数据训练密文模型，并在密文上添加种子生成的随机数

    • client1密文模型“+”随机数

    • client2密文模型“-”随机数

  2. 各client将添加随机数后的密文模型参数发送至server

  3. server将client的密文模型参数进行聚合

  4. server将密文模型参数发送给各client

  5. 各client更新本地的密文模型参数

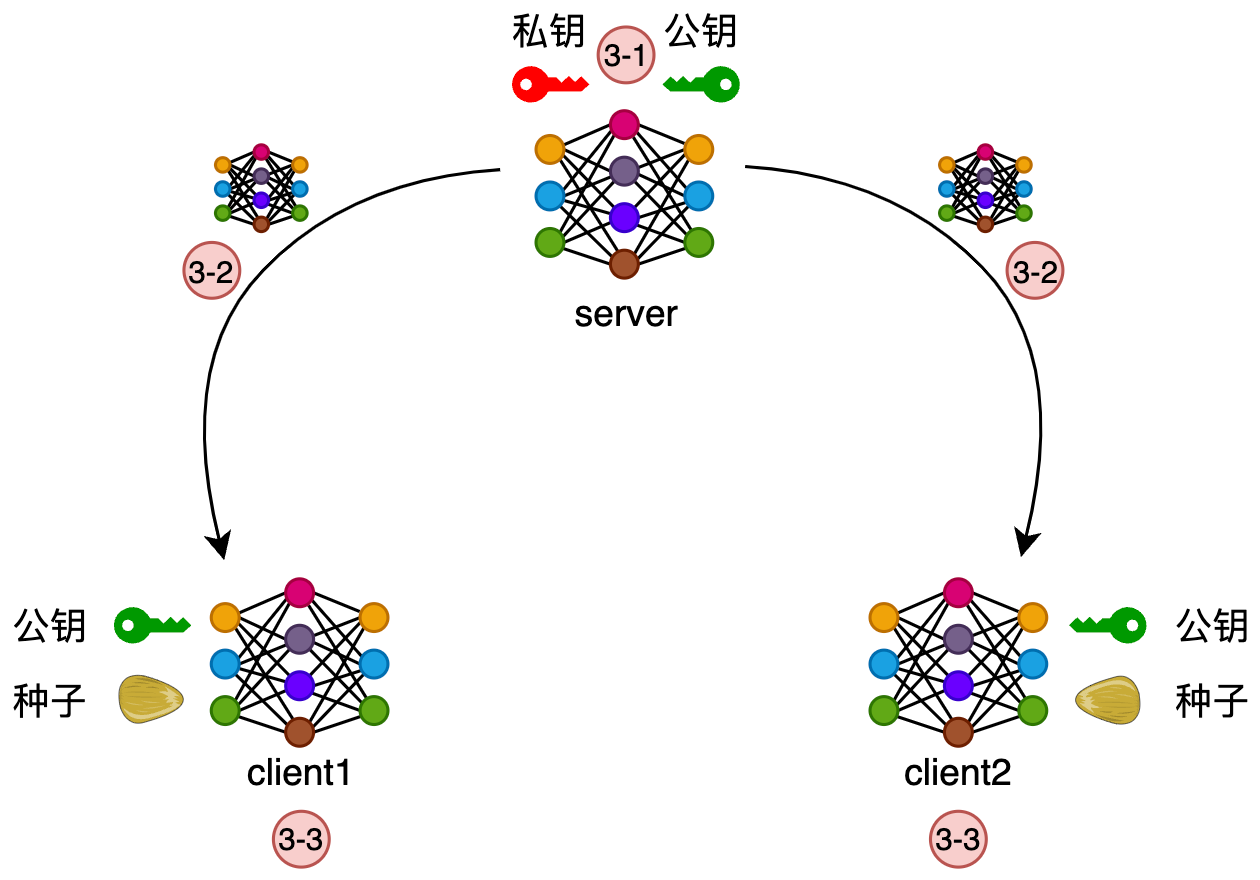
阶段3：模型分发​

  1. server使用私钥将密文模型参数解密

  2. server将明文模型参数发送给各client

  3. 各client更新本地的明文模型参数

3. 梯度和loss近似计算​

  • 由于Paillier不支持密文状态下的乘法、指数、对数、比较运算，因此在计算梯度和loss时需要近似

  • 以Logistic Regression二分类y∈{0,1}y\in\{0,1\}为例，为简化公式，此处省略bb（截距或bias）

3.1 梯度近似计算​

  1. 梯度计算公式

    • sigmoid函数：h(z)=11+e−zh(z)=\frac{1}{1+e^{-z}}，z=ωTxz=\omega^Tx

    • 计算梯度：g=x⋅[h(z)−y]g=x\cdot[h(z)-y]

  2. 梯度近似计算公式

    • 将sigmoid函数在原点进行一阶泰勒展开

      • h′(z)=h[z](1−h(z))h'(z)=h[z](1-h(z))

      • h(z)≈h1(z)=h(0)+h′(0)1!z=12+14zh(z)\approx h_1(z)=h(0)+\frac{h'(0)}{1!}z=\frac{1}{2}+\frac{1}{4}z

    • 计算梯度近似：g=x⋅[h1(z)−y]g=x\cdot[h_1(z)-y]

3.2 loss近似计算​

  1. loss计算公式

    • 计算loss：L(z)=−yln⁡h(z)−(1−y)ln⁡[1−h(z)]\mathcal{L}(z)=-y\ln h(z)-(1-y)\ln[1-h(z)]

  2. loss近似计算公式

    • 将loss函数在原点进行一阶泰勒展开

      • L′(z)=−y[1−h(z)]+(1−y)h(z)=h(z)−y\mathcal{L}'(z)=-y[1-h(z)]+(1-y)h(z)=h(z)-y

      • L(z)≈L(0)+L′(0)1!z=ln⁡2+(12−y)z\mathcal{L}(z)\approx \mathcal{L}(0)+\frac{\mathcal{L}'(0)}{1!}z=\ln2+(\frac{1}{2}-y)z

    • 计算loss近似（去掉常数项）：L(z)≈(12−y)z\mathcal{L}(z)\approx(\frac{1}{2}-y)z

    • 正则化部分的loss无法计算

4. Paillier加解密过程​

4.1 密钥生成​

gcd(x,y)\text{gcd}(x,y)最大公约数，lcm(x,y)\text{lcm}(x,y)最小公倍数，L(x)=x−1nL(x)=\frac{x-1}{n}

  1. 随机且独立选取两个大素数pp和qq，满足gcd(pq,(p−1)(q−1))=1\text{gcd}(pq,(p-1)(q-1))=1

  2. 计算n=pqn=pq和λ=lcm(p−1,q−1)\lambda=\text{lcm}(p-1,q-1)

  3. 随机选取g∈Zn2∗g\in Z^*_{n^2}

  4. 计算μ=(L(gλmod  n2))−1mod  n\mu=(L(g^{\lambda}\mod n^2))^{-1}\mod n，确保μ\mu存在

  5. 公钥：(n,g)(n,g)，私钥：(λ,μ)(\lambda,\mu)

4.2 加密​

假设明文为mm，其范围是0≤ m<n0\le m<n

  1. 选取随机数rr，满足0<r<n0<r<n且gcd(r,n)=1\text{gcd}(r,n)=1

  2. 计算密文c=gm⋅rnmod  n2c=g^m\cdot r^n\mod n^2

4.3 解密​

假设密文为c∈Zn2∗c\in Z^*_{n^2}

  1. 计算明文m=L(cλmod  n2)⋅μmod  nm=L(c^{\lambda}\mod n^2)\cdot\mu\mod n

5. 随机数使用​

由于Paillier计算密文时要模n2n^2，因此添加随机数rr后要模n2n^2

  1. 密文模型参数添加随机数

    • Encr(ω1)=Enc(ω1)+rmod   n2\text{Enc}_r(\omega_1)=\text{Enc}(\omega_1)+r\mod n^2

    • Encr(ω2)=Enc(ω2)−rmod   n2\text{Enc}_r(\omega_2)=\text{Enc}(\omega_2)-r\mod n^2

  2. 随机数抵消

    • Dec(Encr(ω1)+Encr(ω1))=ω1+ω2\text{Dec}(\text{Enc}_r(\omega_1)+\text{Enc}_r(\omega_1))=\omega_1+\omega_2

6. HFL Logistic Regression Paillier运行​

6.1 Training​

  • 如果是通过下载二进制文件或本地编译启动，编译完成后在代码根目录下执行以下命令；如果是通过docker-compose启动，先执行 docker exec -it primihub-node0 bash 进入到 primihub-node0 容器中，再执行以下命令。
./primihub-cli --task_config_file="example/FL/logistic_regression/hfl_binclass_paillier.json"
  • 或者通过Python SDK启动
submit example/FL/logistic_regression/hfl_binclass_paillier.json

6.2 Prediction​

  • 下载二进制文件、本地编译、docker-compose启动
./primihub-cli --task_config_file="example/FL/logistic_regression/hfl_binclass_predict.json"
  • Python SDK启动
submit example/FL/logistic_regression/hfl_binclass_predict.json

7. 参考文献​

  1. https://en.wikipedia.org/wiki/Paillier_cryptosystem

  2. https://en.wikipedia.org/wiki/NIST_SP_800-90A

注：随机数暂未添加​

Was this page helpful?

Happy React is loading...