横向联邦DP-SGD算法
1. 简介
训练时对梯度剪裁后添加噪声
称为隐私预算,越小安全性越高
2. 符号说明
| 符号 | 说明 |
|---|---|
| 梯度 | |
| 第个样本的梯度 | |
| 第个样本剪裁后的梯度 | |
| 添加噪声后的梯度 | |
| batch size | |
| 导数 | |
| 模型参数 | |
| 损失函数 | |
| 特征 | |
| 第个样本的特征 | |
| 标签 | |
| 第个样本的标签 | |
| 学习率 | |
| 范数 | |
| 剪裁阈值 | |
| 高斯噪声 | |
| 噪声参数 |
3. SGD和DP-SGD算法对比
3.1 SGD算法步骤
计算一个batch数据的梯度并取均值
更新模型参数
3.2 DP-SGD算法步骤
计算单样本的梯度
单样本梯度剪裁
梯度中添加噪声
高斯噪声的方差取决于和的乘积
隐私预算仅取决于参数,与无关
更新模型参数
4. DataLoader对比
4.1 DataLoader
每次根据batch size,序列化选取批量数据,取完后对数据洗牌
4.2 DPDataLoader
每次根据采样率进行有放回泊松采样,选取批量数据
5. DP超参数的影响
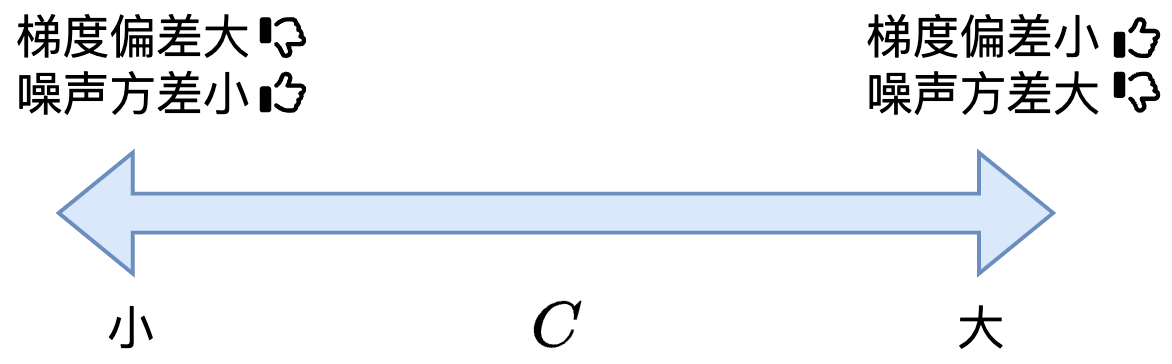
5.1 剪裁阈值
影响梯度偏差和噪声的方差,但不影响隐私预算的大小
越小,对梯度的剪裁力度越大,引入的偏差越大
无梯度剪裁时,将一个batch中各样本梯度累加
剪裁阈值偏大时,范数较大的梯度被剪裁,其余梯度不变,累加后的梯度偏差较小
剪裁阈值偏小时,大部分梯度被剪裁,累加后的梯度偏差较大
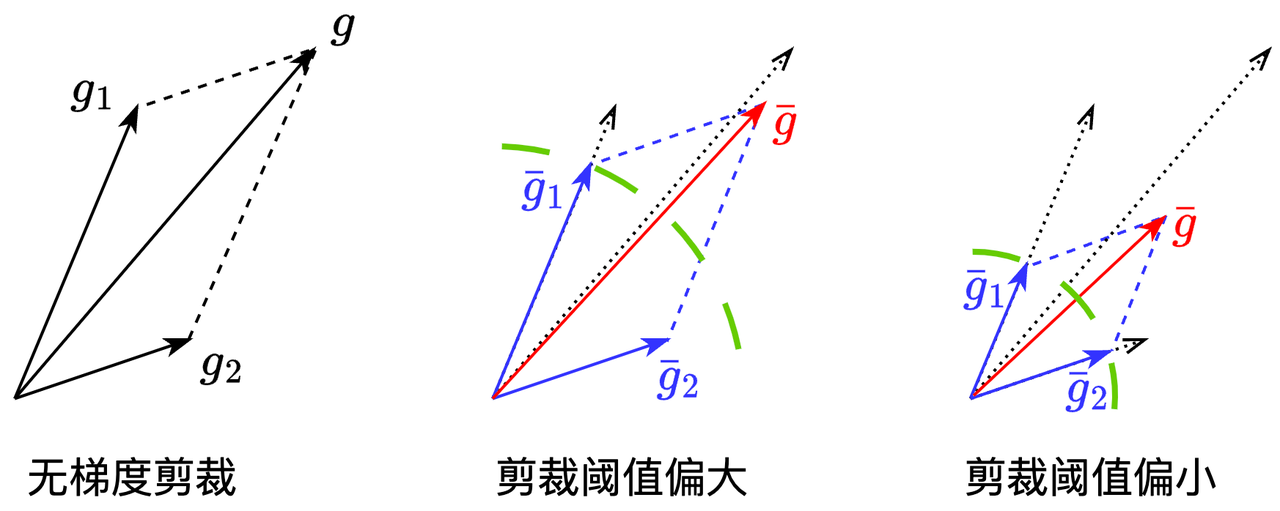
越小,噪声的方差越大,添加的噪声越大
计算隐私预算不需要参数,故不影响隐私预算的大小
5.2 噪声参数
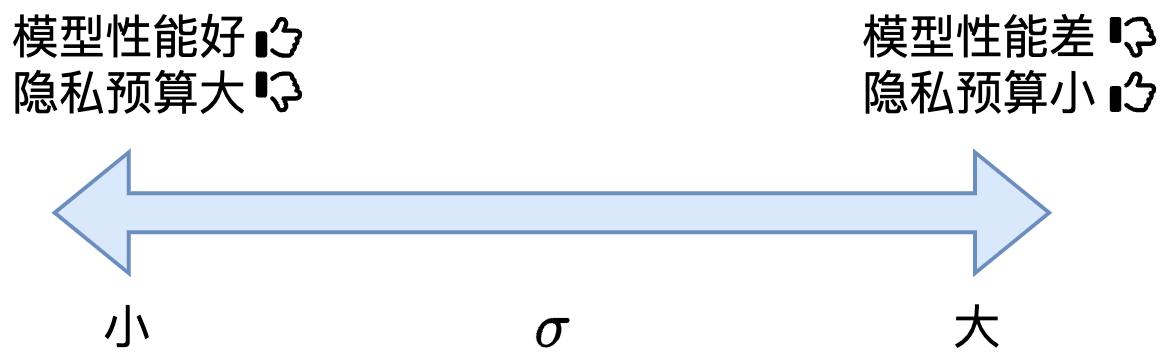
影响模型的性能和隐私预算的大小
越小,噪声越小,模型性能越好
越小,隐私预算越大,安全性越弱
6. 隐私预算的计算
安装:
pip install dp-accounting参数解释
steps: 训练迭代次数,等于epoch * num_train_examples // batch_sizenoise_multiplier: 高斯噪声参数num_train_examples: 训练样本数量delta: -DP中的参数,需满足sampling_probability:采样率,等于batch size /
参数对隐私预算大小的影响
训练迭代次数越多,隐私预算越大
高斯噪声参数越小,隐私预算越大
DP参数越小,隐私预算越大
采样率越大,隐私预算越大
batch size影响训练迭代次数和采样率:batch size增大,训练迭代次数减少,采样率增大。一般来说采样率对隐私预算的影响大,因此batch size增大,隐私预算一般增大
训练样本数量影响训练迭代次数和采样率:样本数量减少,训练迭代次数减少,采样率增加。一般来说采样率对隐私预算的影响大,因此样本数量减少,隐私预算一般增大
代码样例
import dp_accounting
import logging
noise_multiplier = 1.0
batch_size = 256
num_train_examples = 60000
delta = 1e-5
def compute_epsilon(steps):
"""Computes epsilon value for given hyperparameters."""
if noise_multiplier == 0.0:
return float('inf')
orders = [1 + x / 10. for x in range(1, 100)] + list(range(12, 64))
accountant = dp_accounting.rdp.RdpAccountant(orders)
sampling_probability = batch_size / num_train_examples
event = dp_accounting.SelfComposedDpEvent(
dp_accounting.PoissonSampledDpEvent(
sampling_probability,
dp_accounting.GaussianDpEvent(noise_multiplier)), steps)
accountant.compose(event)
if delta > 1. / num_train_examples:
logging.error(f"delta {delta} should be set less than 1 / {num_train_examples}")
return accountant.get_epsilon(target_delta=delta)
7. 安全浮点数噪声生成
使用:设置'secure_mode'为True
sum(gauss(0, 1) for i in range(2 * n)) / sqrt(2 * n)- 原理:高斯分布累加后还是高斯分布
n>1,根据效率和计算复杂性考虑,一般取n=2
8. HFL Logistic Regression DP-SGD运行
8.1 Training
- 如果是通过下载二进制文件或本地编译启动,编译完成后在代码根目录下执行以下命令;如果是通过docker-compose启动,先执行
docker exec -it primihub-node0 bash进入到primihub-node0容器中,再执行以下命令。
./primihub-cli --task_config_file="example/FL/logistic_regression/hfl_binclass_dpsgd.json"
- 或者通过Python SDK启动
submit example/FL/logistic_regression/hfl_binclass_dpsgd.json
8.2 Prediction
- 下载二进制文件、本地编译、docker-compose启动
./primihub-cli --task_config_file="example/FL/logistic_regression/hfl_binclass_predict.json"
- Python SDK启动
submit example/FL/logistic_regression/hfl_binclass_predict.json
9. 参考文献
Abadi, Martin, Andy Chu, Ian Goodfellow, H. Brendan McMahan, Ilya Mironov, Kunal Talwar, and Li Zhang. "Deep learning with differential privacy." In Proceedings of the 2016 ACM SIGSAC conference on computer and communications security, pp. 308-318. 2016. https://arxiv.org/pdf/1607.00133.pdf
Mironov, Ilya, Kunal Talwar, and Li Zhang. "Renyi differential privacy of the sampled gaussian mechanism." arXiv preprint arXiv:1908.10530 (2019). https://arxiv.org/pdf/1908.10530.pdf
Holohan, Naoise, and Stefano Braghin. "Secure random sampling in differential privacy." In European Symposium on Research in Computer Security, pp. 523-542. Springer, Cham, 2021. https://arxiv.org/pdf/2107.10138.pdf