纵向联邦XGBoost

纵向联邦学习及其应用场景

定义

在数据集上具有相同的样本空间、不同的特征空间的参与方所组成的联邦学习归类为纵向联邦学习（Vertical Federated Learning，VFL），也可以理解为按特征划分的联邦学习。

场景

作为一种保护隐私的分布式训练技术，联邦学习近几年成为学术界研究的热点话题，很多研究关于联邦学习的效率、安全性、隐私性展开讨论。最近在企业中联邦学习的应用也逐渐开展，按照参与方数据分布的差异，联邦学习通常可以分为横向联邦学习(HFL)、纵向联邦学习(VFL)以及联邦迁移学习。相较于横向联邦学习，纵向联邦学习在实际企业中应用更加广泛，它通常适用于不用部门之间数据垂直分布的场景，例如：政务开放、医疗应用、金融应用、数字广告、物流行业等。

XGBoost原理

目标函数

原始目标函数

原始目标函数分为两个部分：一部分是损失函数，一部分是正则（用于控制模型的复杂度）。

对于第t棵树，第i个样本，模型的预测值为:$\hat{y}_{i}^{t}=\sum_{k=1}^{t}f_{k}(x_{i})=\hat{y}_{i}^{t-1}+f_{t}(x_{i})$。

注：其中$\hat{y}_{i}^{t}$是第t次迭代之后样本i的预测结果；$f_{t}(x_{i})$是第t棵树的模型预测结果；$\hat{y}_{i}^{t-1}$是第t-1棵树的预测结果。

进一步可以得到原始的目标函数：$Obj=\sum_{i=1}^{n}l(y_{i},\hat{y}_{i})+\sum_{j=1}^{t}\Omega (f_{j})$

注：其中$`l(y_{i},\hat{y}_{i})`$是模型的损失函数；$`\hat{y}_{i}`$是整个模型对第i个样本的预测值；$`y_{i}`$是第i个样本的真实值；$`\sum_{j=1}^{t}\Omega (f_{j})`$是t棵树的复杂度求和（理解为正则化项）

简化目标函数

由于XGBoost是前向迭代，可以将涉及到的前t-1个树变量或者参数看作常数，所以对目标函数进行如下简化：

$$Obj=\sum_{i=1}^{n}l(y_{i},\hat{y}_{i}^{t})+\sum_{j=1}^{t}\Omega (f_{j})=\sum_{i=1}^{n}l(y_{i},\hat{y}_{i}^{t-1}+f_{t}(x_{i}))+\sum_{j=1}^{t}\Omega (f_{j})=\sum_{i=1}^{n}l(y_{i},\hat{y}_{i}^{t-1}+f_{t}(x_{i}))+\Omega (f_{t})+constant$$

泰勒公式对目标函数近似展开

基本泰勒公式展开如下:

$$f(x+\Delta x)\simeq f(x)+f'(x)\Delta x+\frac{1}{2}f''(x)\Delta x^{2}$$

将损失函数进行泰勒公式二阶展开，结果为：$l(y_{i},\hat{y}_{i}^{t-1}+f_{t}(x_{i}))\simeq l(y_{i},\hat{y}_{i}^{t-1})+g_{i}f_{t}(x_{i})+\frac{1}{2}h_{i}f_{t}^{2}(x_{i})$

注：$g_{i}$对应的是损失函数一阶导数，$h_{i}$对应的是损失函数二阶导数

进而可以得到目标函数展开公式如下： $Obj\simeq \sum_{i=1}^{n}[l(y_{i},\hat{y}_{i}^{t-1})+g_{i}f_{t}(x_{i})+\frac{1}{2}h_{i}f_{t}^{2}(x_{i})]+\Omega (f_{t})+constant$

树的参数化

树模型参数化

• 每棵树每个叶子节点的值（即每个叶子节点的权重）w
• 样本到叶子节点的映射关系（即每个样本落在当前这棵树的哪一个叶子节点上）q
• 叶子节点样本归属集合I

树的复杂度参数化

• 每个树的叶子节点的个数
• 叶子节点的权重值

树的复杂度表达式如下：$\Omega(f_{t})=\gamma T+\frac{1}{2}\lambda \sum_{j=1}^{T}\omega _{j}^{2}$

注：T为当前这棵树叶子节点的个数；$\omega _{j}^{2}$为叶子节点值的$L_{2}$范数

Hetero XGB

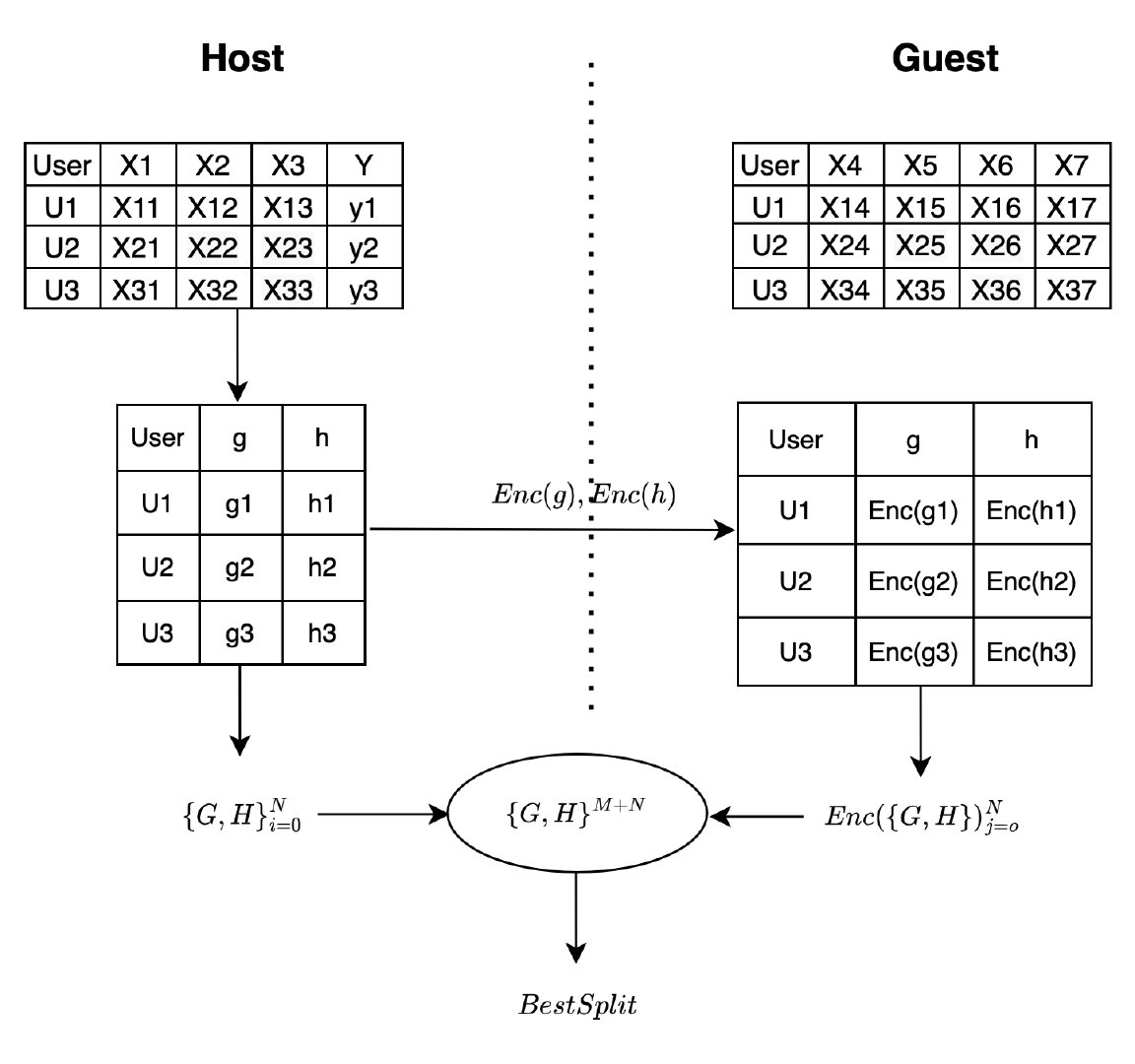
算法流程

Host端：数据中拥有标签的一方

Guest端：数据中没有标签的一方

1. Host端基于自研高性能Paillier库以及随机种子生成公私钥，并将公钥发送给Guest端；
2. Host端基于当前预测值和Label进行计算一阶导数与二阶导数，并将一阶与二阶导数进行半同态加密，然后发送至Guest端；
3. Host端根据己端数据，计算Host_Best_Gain，同时Guest端计算所有可能的Guest_Best_Gain，并将Guest_Best_Gain加密后发送给Host端；
4. Host端将从Guest端获取的加密Guest_Best_Gain进行解密，得到解密后的Guest_Best_Gain；
5. 在Host端比较Host_Best_Gain与Guest_Best_Gain的大小，确定XGB树的最优分裂点；
6. 重复步骤3、4、5，直到模型收敛或达到迭代最大次数，模型训练完成。

简化流程示意图

Hetero_XGB算法优化

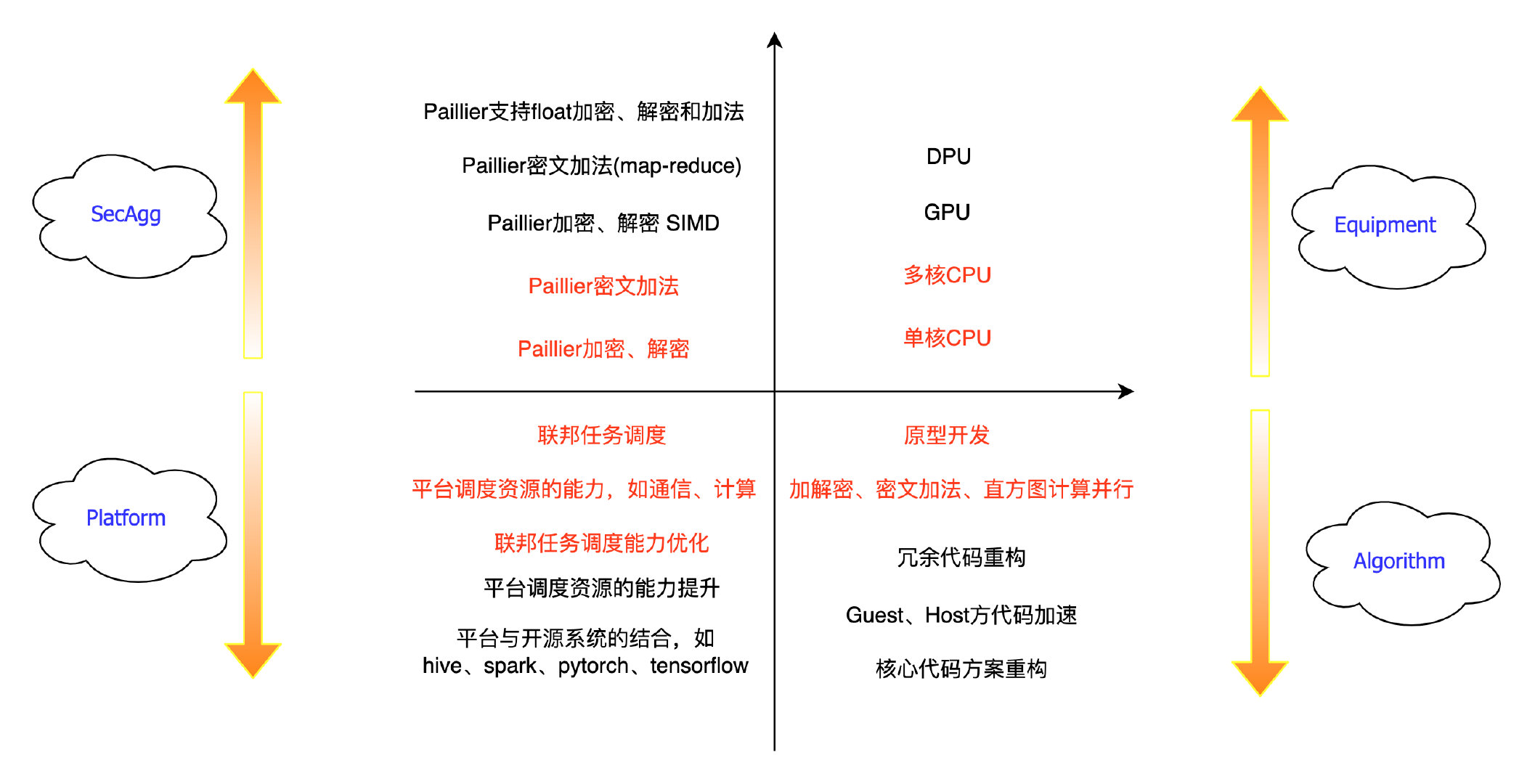
优化亮点

1. 基于Ray的并行加速；
2. 采用python底层的加速函数；
3. 自研高性能Pallier库；
4. 平衡Host与Guest端的计算资源，提高计算效率。

Primihub Hetero XGB运行

Hetero XGB Training

提交联邦学习任务的参数说明

创建联邦学习任务需要使用以下参数组合 --task_lang=python --task_type=0, 并通过task_code参数指定要运行的联邦学习python代码。

• 如果是通过下载二进制文件或本地编译启动，编译完成后在代码根目录下执行以下命令；如果是通过docker-compose启动，先执行 docker exec -it primihub-node0 bash 进入到 primihub-node0 容器中，再执行以下命令。

./primihub-cli --task_config_file="example/FL/xgboost/hetero_xgb.json"

• 或者通过Python SDK启动

submit example/FL/xgboost/hetero_xgb.json

提示

如果遇到报错 "No module named 'primihub'", 在代码根目录下执行以下命令安装 primihub 平台库

cd python
pip3 install -r requirements.txt
python3 setup.py install --user

Hetero XGB Prediction

• 下载二进制文件、本地编译、docker-compose启动

./primihub-cli --task_config_file="example/FL/xgboost/hetero_xgb_infer.json"

• Python SDK启动

submit example/FL/xgboost/hetero_xgb_infer.json

参数说明

参数	数据类型	参数示例	参数说明
params.predictFileName	STRING	/data/result/prediction.csv	预测结果文件，仅出现在Host方
params.indicatorFileName	STRING	/data/result/indicator.json	模型评估指标结果文件，仅出现在Host方
params.hostLookupTable	STRING	/data/result/hostlookuptable.csv	Host方特征分割点结果文件
params.guestLookupTable	STRING	/data/result/guestlookuptable.csv	Guest方特征分割点结果文件
params.modelFileName	STRING	/data/result/host/model	树结构保存路径，仅出现在Host方

参考文献

SecureBoost: A Lossless Federated Learning Framework：https://arxiv.org/pdf/1901.08755.pdf

XGBoost Tutorials：https://xgboost.readthedocs.io/en/latest/tutorials/index.html

Federated Machine Learning: Concept and Applications：https://arxiv.org/pdf/1902.04885.pdf